Complexity

Jun 2, 2025

What is Complexity

The complexity of an algorithm is a measure of the resources required to run it. The factors regarding the input are closely related to complexity, often indicated by alphabets such as n and m.

For example, if a one-dimensional array is the input, its size, such as n, is a crucial factor.

Big O Notation

Big O is a mathematical notation used to describes the limiting behavior of a function when the argument tends towards infinity. In other words, Big O represents the order of growth of a function.

When calculating Big O, it only cares about the dominant terms. For instance, consider a function f(n) = 2n² + 3n + 100. If n is very large, or even infinite, coefficients such as 2 at the highest term and lower terms like 3n and 100 aren't important because they don't significantly affect the result, even without considering them. Therefore, O(f(n)) = O(n²).

In math, there are many asymptotic notations, but Big O is widely used in computer science.

Definition

Big O is defined as asymptotic upper bound or the worst case.

f(N) = O(g(N)), if there exist positive constants c, N₀ such that
f(N) <= C, g(N) for all N >= N₀ 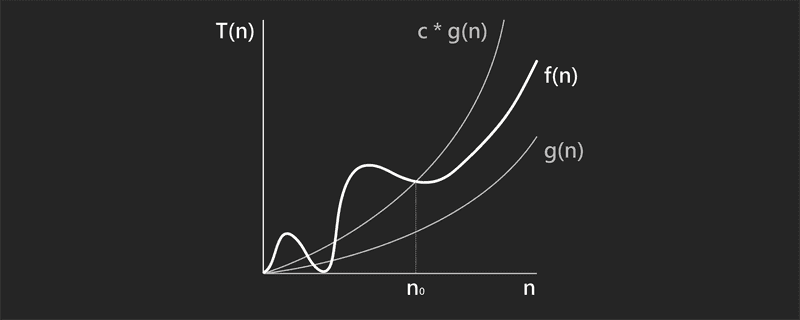Lingo: "f(N) grows no faster than g(N)."

Order

1 < log n < √n < n < n log n < n² < n³ < 2ⁿ < 3ⁿ < n! < nⁿ

INPUT	1	n	n²	2ⁿ	n!	nⁿ
1	1	1	1	1	1	1
2	1	2	4	4	2	4
3	1	3	9	8	6	27
4	1	4	16	16	24	256
5	1	5	25	32	120	3,125
6	1	6	36	64	720	46,656
7	1	7	49	128	5,040	823,543
8	1	8	64	256	40,320	16,777,216
9	1	9	81	512	362,880	387,420,489
10	1	10	100	1,024	3,628,800	1,000,000,000

Time Complexity

Time complexity refers to estimating the duration of an algorithm's execution based on the number of operations it performs.

Below is a function code including an array parameter with n elements. It runs a for loop which contains three lines of operations n times. Thus, its time complexity is O(n * (1 + 1 + 1)) = O(n).

def print_all_elements(array):
    for index in range(len(array)):  # loop: n times
        print(array[index])          # line: 1
        if index == len(array)-1:    # line: 1
            print('--- End ---')     # line: 1
python

Space Complexity

Space complexity refers to estimating the total space required by the algorithm.

Below is a function code including a number parameter, n. It runs a for loop which allocates a new space n times and perform other operations without additional space. Thus, its space complexity is O(0 + n * 1 + 0) = O(n).

def list_all_positive_numbers(n):
    array = []                       # space: 0
    for num in range(n):             # loop:  n times
        array.append(num)            # space: 1
    return array                     # space: 0
python

In-place

In-place means that an algorithm operates directly on the space of input parameters without requiring additional space relative to the input factors. The strict definition includes O(1) space complexity.